Entering a formula in Math 3x

You can enter a formula in three ways:

• Select a symbol from the Formula Elements window.
• Right-click on the equation editor and select the symbol from the context menu.
• Type markup in the equation editor.

The context menu and the Formula Elements window insert the markup corresponding to a symbol. This provides a convenient way to learn the OOoMath markup.

Click on the document body to exit the formula editor. Double-click on a formula to enter the formula editor again.

The Formula Elements window

The simplest method for entering a formula is to use the Formula Elements window, shown below.

Symbols are divided into categories

The Formula Elements window is divided into two main portions.

• The top shows the symbol categories. Click on these to change the list of symbols.
• The bottom shows the symbols available in the current category.

You can hide or show the Formula Elements window with View > Formula Elements.

Example 1: 5 × 4

For this example we will enter a simple formula: 5 × 4. On the Formula Elements window:

1. Select the top-left button of the categories (top) section.
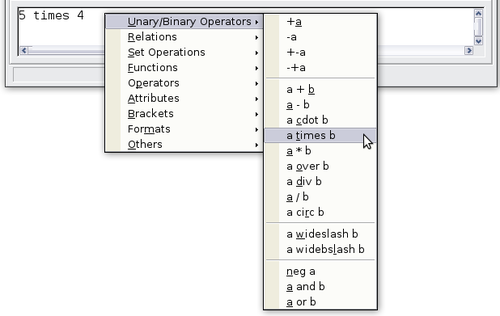
2. Click on the multiplication symbol.

Selecting the multiplication symbol

When you select the multiplication symbol on the Formula Elements window, two things happen:

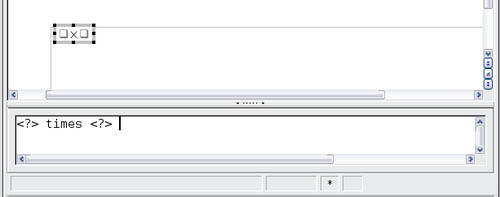
• The equation editor shows the markup: <?> times <?>
• The body of the document shows a gray box containing symbols like this: $\Box \times \Box$

Result of selecting the multiplication symbol

The <?> symbols are placeholders that you can replace by other text, for example 5 and 4. The equation will update automatically, and the result should resemble the figure below.

Result of entering 5 and 4 next to the times operator

To keep the equation from updating automatically, choose View > AutoUpdate display from the menu bar. To update a formula manually, press F9 or choose View > Update.

Right-click menu

Another way to access mathematical symbols is to right-click on the equation editor. This pops up the menu shown below. The entries in this menu correspond exactly to those in the Formula Elements window.

Right-click menu.

Markup

You can type the markup directly in the equation editor. For example, you can type “5 times 4" to obtain $5\times 4$. If you know the markup, this can be the fastest way to enter a formula.

The formula markup resembles the way the formula reads in English.

Below is a short list of common equations and their corresponding markup.

Display	Command	Display	Command
a=b	a = b	√a	sqrt {a}
a2	a^2	an	a_n
∫ f(x)dx	int f(x) dx	∑ an	sum a_n
a≤b	a <= b	∞	infinity
a×b	a times b	x·y	x cdot y

Greek characters

Greek characters (α, β, γ, θ, etc.) are common in mathematical formulas. These characters are not available in the Formula Elements window or on the right-click menu. Fortunately, the markup for Greek characters is simple: Type a % sign followed by the name of the character, in English.

• To write a lowercase character, type the name of the character in lowercase.
• To write an uppercase character, type the name of the character in uppercase.

See the table below for some examples.

Lowercase	Uppercase
%alpha α	%ALPHA Α
%beta β	%BETA Β
%gamma γ	%GAMMA Γ
%psi ψ	%PSI Ψ
%phi φ	%PHI Φ
%theta θ	%THETA Θ

A complete table of Greek characters is included in the Math Object chapter in the Writer Guide.

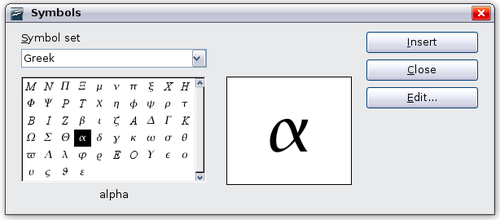
Another way to enter Greek characters is by using the catalog window. Go to Tools > Catalog. The catalog window is shown below. Under “Symbol Set" select “Greek" and double-click on a Greek letter from the list.

Symbols catalog, used for entering Greek characters.

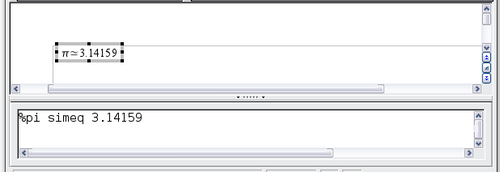
Example 2: π $\simeq \!$ 3.14159

For this example we will suppose that:

• We want to enter the above formula (the value of pi rounded to 5 decimal places).
• We know the name of the Greek character ("pi").
• But we do not know the markup associated with the $\simeq \!$ symbol.

Step 1: Type "%" followed by the text "pi". This displays the Greek character π.

Step 2: Open the Formula Elements window (View > Formula Elements).

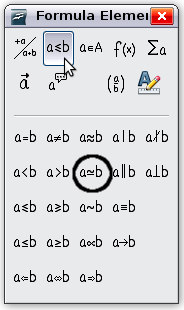
Step 3: The $\simeq \!$ symbol is a relation, so we click on the Relations button . If you hover the mouse over this button you see the tooltip "Relations".

Tooltip indicates the Relations button.

The figure below shows the Formula Elements window after clicking the Relations button. The symbol we want is circled.

After selecting Relations.

Step 4: Click on the a$\simeq \!$b symbol. The equation editor now shows the markup %pi<?> simeq <?>.

Step 5: Delete the <?> text and add "3.14159" at the end of the equation. We end up with the markup %pi simeq 3.14159. The result is shown below.

Final result.