Matrices gebruiken
Introductie
Matrices kunnen handig zijn bij het reduceren van het aantal cellen dat u gebruikt, maar ze kunnen ietwat ingewikkeld te begrijpen zijn. Op sommige manieren kunnen zij de mogelijkheden van een werkblad uitbreiden tot voorbij het punt waarvoor werkbladen bedoeld waren. Bijna alle taken zijn mogelijk zonder hen.
Een matrix (array) is eenvoudigweg een rechthoekig blok van informatie dat Calc kan bewerken in een formule - dat betekent dat het informatie is die is georganiseerd in rijen en kolommen. Een matrix kan cellen zijn op een werkblad of intern door Calc worden behandeld.
Er zijn 2 manieren om een matrix in een formule te specificeren:
- als een bereik - bijvoorbeeld A2:C3.
- als een "matrix als regel", bijvoorbeeld {1; 5; 3 | 6; 2; 4} (deze zijn volledig functioneel vanaf OOo2.4, maar zij bestaan in eerdere versies - zie Matrix-problemen). U typt accolades { } rondom een matrix als regel. Items op een regel worden gescheiden door een punt-komma ‘;’, en rijen worden gescheiden door het teken pipe ‘|’. Elke rij moet hetzelfde aantal elementen hebben (het is niet juist om te schrijven {1; 2; 3 | 4; 5} omdat er 3 elementen in de bovenste rij staan en slechts 2 in de volgende rij). Matrices als regel mogen gemixte inhoud hebben, bijvoorbeeld {4; 2; "hond" | -22; "kat"; 0}. Een matrix als regel mag echter geen verwijzingen bevatten (bijv.: A4), of formules (bijv.: PI(), 2*3 ), of percentages (bijv.: 5%).
U kunt een naam geven aan een celbereik: selecteer het bereik en kies Invoegen → Namen → Definiëren.
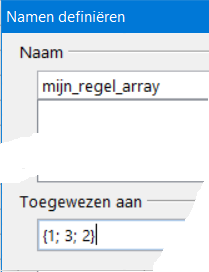
U kunt een naam geven aan een matrix als regel: kies Invoegen → Namen → Definiëren; type de matrix (bijv.: {1; 3; 2} inclusief de accolades) in het vak Toegewezen aan.
Functies die matrices als parameters begrijpen
Sommige functies, zoals SOM(), GEMIDDELDE(), VERGELIJKEN() en ZOEKEN(), accepteren één of meer van hun parameters als matrices.
Bijvoorbeeld:
- SOM( A2:C3 ) geeft de som terug van de getallen in het bereik A2:C3.
- SOM( {3; 2; 4} ) geeft 9 terug, de som van de getallen in matrix als regel {3; 2; 4}.
- SOM verwacht/begrijpt ook enkele (‘scalaire’) waarden - SOM( B5; 7 ) geeft de som terug van B5 en 7.
Functies die geen matrix als parameter verwachten
Sommige functies, zoals ABS(), WORTEL(), COS(), LENGTE() verwachten dat hun parameters ‘scalair’ zijn - dat betekent één enkele waarde zoals 354 of "hond" of de inhoud van een cel bijv.: B5.
Voorbeelden:
- WORTEL(4) geeft 2 terug.
- LENGTE("hond") geeft 4 terug.
U kunt echter nog steeds een matrix gebruiken waar één enkele waarde wordt verwacht - bijvoorbeeld WORTEL( {9; 4} ). Als u de formule invoert door ‘normaal’ op ↵ Enter te drukken, zal Calc de formule als volgt evalueren met behulp van één enkele waarde uit de matrix.
Als het een matrix als regel is:
- Calc zal de eerste waarde gebruiken (die ‘linksboven’).
- Voorbeeld:
- =WORTEL( {9; 4 | 25; 16} ) drukken op ↵ Enter geeft 3 terug, de wortel van het eerste element in de matrix (9).
Als het een bereik is:
- 1. Calc zal een fout teruggeven, tenzij de matrix één enkele rij of één enkele kolom is.
- 2. Voor een bereik van één enkele rij of één enkele kolom zal Calc de waarde gebruiken van de cel waar de kolom/rij van de formule-cel kruist met de matrix (of een fout teruggeven als er geen kruising is).
- Voorbeelden:

- De formule =ABS(B2:B5) wordt 'normaal' ingevoerd in cel D3, dat is op rij 3. Rij 3 kruist B2:B5 bij cel B3, dus de geëvalueerde formule is =ABS(B3).
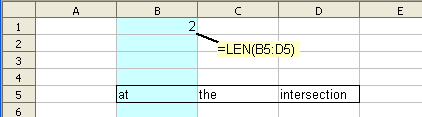
- De formule =LENGTE(B5:D5) wordt 'normaal' ingevoerd in cel B1, dat is in kolom B. Kolom B kruist B5:D5 bij cel B5, dus de geëvalueerde formule is =LENGTE(B5).
Matrixformules
De echte kracht van matrices komt als u een formule op een speciale manier invoert, als een ‘matrixformule’. U doet dit door op Ctrl + ⇧ Shift + ↵ Enter te drukken in plaats van op de toets ↵ Enter (of door het vakje Matrix te selecteren als u de Functie-assistent gebruikt).
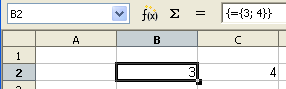
Als u in cel B1 ‘normaal’ invoert ={3; 4} door op ↵ Enter te drukken, wordt de eerste waarde 3 weergegeven in de cel.
Als u in cel B2 invoert ={3; 4} maar drukt op Ctrl + ⇧ Shift + ↵ Enter in plaats van op ↵ Enter , wordt de cel een 'matrixformule'. De formule geeft nu de gehele matrix {3; 4} terug. Cel B2 geeft 3 weer en cel C2 geeft 4 weer.
- Let er op dat als u de formule invoerde door op de toets ↵ Enter te drukken, het eenvoudigweg selecteren van de cel en te drukken op Ctrl + ⇧ Shift + ↵ Enter de cel niet zal converteren naar een matrix-expressie - u moet echt een bewerking uitvoeren (zoals een teken toevoegen of verwijderen), of op de Functie-assistent klikken en het vakje Matrix selecteren.
Als u nu probeert om de cel B2 te bewerken, krijgt u een melding dat "u geen deel van een matrix kunt bewerken". U moet de gehele matrix selecteren om die te bewerken, ofwel met de muis of door te typen Ctrl-/ (houd de Ctrl -toets ingedrukt en druk op de slash-toets / ).
De formulebalk geeft aan dat dit een matrixformule is door die met accolades te omsluiten {}. U hoeft die niet te typen - zij zullen verdwijnen als u de formule bewerkt, en Calc zal ze opnieuw weergeven als u gereed bent met bewerken.
Berekeningen met matrixformules
Als Calc een matrixformule evalueert, behandelt het ‘onverwachte matrices’ als een serie van waarden (in plaats van één enkele waarde te gebruiken), berekent een resultaat voor elk van de matrix-elementen en geeft een resultaten-matrix weer.
Voorbeeld:
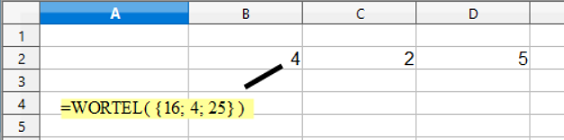
- =WORTEL( {16; 4; 25} ) ingevoerd met het drukken op Ctrl-Shift-Enter in plaats van Enter geeft een resultaten-matrix weer, met 1 rij en 3 kolommen - {4; 2; 5}. Als de formule in cel B2 staat, plaatst Calc de resultaten in de cellen B2:D2. 4 wordt geplaatst in B2, 2 in C2 en 5 in D2.
Het uitgevoerde proces werkt aldus:
- Alle ‘onverwachte matrices’ in dezelfde matrix-berekening zouden dezelfde afmetingen moeten hebben (zie dit issue: Issue 46681).
- Het resultaat zal worden teruggegeven in een matrix van die afmeting.
- De berekening wordt, op zijn beurt, gedaan voor elk element, waarbij het resultaat wordt teruggegeven in het corresponderende element van de uitvoer-matrix.
Voorbeeld:
Met de matrixformule =WORTEL( {16; 4; 25} ):
- Er is slechts één matrix, met 1 rij en 3 kolommen.
- Het resultaat zal worden teruggeven in een matrix met 1 rij en 3 kolommen.
- De berekening wordt eerst gedaan voor 16, dan voor 4, dan voor 25, wat de resultaat-matrix {4; 2; 5} oplevert.
Voorbeeld:
Met de matrix-formule =WORTEL( {8 | 18} * 2 ) in cel A5:
- Er is slechts één matrix, met 2 rijen en 1 kolom.
- Het resultaat zal worden teruggeven in een matrix met 2 rijen en 1 kolom.
- De berekening is: eerste element WORTEL(8*2) = 4; tweede element WORTEL(18*2) = 6; de resultaat-matrix is dus {4 | 6} - dat betekent 4 in cel A5 en 6 in cel A6.
Het resultaat van een matrix-expressie is een matrix, die kan worden gebruikt binnen de formule.
Voorbeeld:
- =SOM(WORTEL( {16; 4; 25} )) als een matrixformule. De berekening van WORTEL( {16; 4; 25} ), als hiervoor, levert als resultaat op {4; 2; 5}, dus geeft SOM( {4; 2; 5} ), levert als totaalresultaat in de cel op van 4+2+5 = 11.
Voorbeeld:
Met de matrixformule =SOM(ALS(A1:A4>0; B1:B4; 0))
- De twee matrices A1:A4 en B1:B4 hebben beide 4 rijen en 1 kolom.
- Het resultaat van de ALS()-matrixberekening zal een matrix zijn van die afmeting, die SOM() zal optellen.
- Als A1>0 het eerste element is B1; anders 0. Als A2>0 het tweede element is B2; anders 0 .... De aan SOM() gepresenteerde matrix heeft de waarden in B1:B4 waar de aanliggende waarde in A1:A4 is >0. De uiteindelijke uitvoer is de som van de waarden in B1:B4 waarvoor de aanliggende waarde in A1:A4 is >0.
Matrixfuncties
Sommige functies berekenen hun resultaten als een matrix. Als zij die matrix moeten teruggeven, moeten zij worden ingevoerd als een matrixformule, door te drukken op Ctrl + ⇧ Shift + ↵ Enter (of door het vakje Matrix te selecteren als u de Functie-assistent gebruikt). Als ze, in plaats daarvan, ze 'normaal' worden ingevoerd met de ↵ Enter -toets, zal alleen het (enkele) element linksboven van de berekende matrix worden teruggegeven. Deze functies worden opgesomd in de categorie Matrixfuncties, en zijn:
Bijvoorbeeld: =EENHEIDSMAT(2) ingevoerd als een matrixformule in cel B1 geeft de eenheid 2 x 2 (identiteit) matrix als de matrix {1; 0 | 0; 1} - dat betekent, cellen B1, B2, C1, C2 tonen 1, 0, 0, 1. Als deze formule 'normaal' wordt ingevoerd, wordt alleen de waarde van 'linksboven' (1) weergegeven in cel B1.
Sommige functies (inclusief enkele die hierboven zijn vermeld) accepteren parameters die worden gedwongen te evalueren als een matrixformule, zelfs als de formule 'normaal' wordt ingevoerd:
- DETERMINANT.MAT, INVERSEMAT, PRODUCTMAT, SOMPRODUCT, SOM.X2MINY2, SOM.X2PLUSY2, SOM.XMINY.2, CORRELATIE, COVARIANTIE, VOORSPELLEN, F.TOETS, SNIJPUNT, MODUS, PEARSON, KANS, R.KWADRAAT, STIJGING, STFOUTYX, T.TOETS
Bijvoorbeeld: MODUS(ABS(A1:A3)) (in normale modus) forceert dat ABS(A1:A3) wordt geëvalueerd als een matrixformule, die een matrix teruggeeft van de absolute waarden van A1:A3 van waaruit MODUS de meest algemene waarde selecteert om te worden teruggegeven.
Bijvoorbeeld: KANS(A1:A5; B1:B5/100; 3) (in normale modus) forceert dat B1:B5/100 wordt geëvalueerd als een matrixformule, die een matrix teruggeeft waarin elke waarde één honderdste van zijn waarde in B1:B5 is (misschien omdat de kansen werden uitgedrukt in procenten).
Een aantal van deze functies hebben enkele (matrix)-parameters die worden geforceerd om te worden geëvalueerd als een matrixformule, en andere (enkele waarde)-parameters die normaal evalueren.
Bijvoorbeeld: KANS(A1:A5; B1:B5; {3; 4}) (in normale modus) evalueert {3; 4} niet als een matrix, omdat dit zou betekenen dat KANS een matrix teruggeeft. Het evalueert KANS(A1:A5; B1:B5; 3) - dat betekent, het interpreteert {3; 4} in scalaire modus, door de waarde 'linksboven' 3 te nemen. Indien het echter wordt ingevoerd als een matrixformule, zal het natuurlijk een matrix teruggeven.
Tips en trucs
Al deze voorbeelden moeten worden ingevoerd als een matrix-expressie, door op Ctrl + ⇧ Shift + ↵ Enter te drukken.
Som van items die overeenkomen met meerdere voorwaarden
SOM( (A1:A6="rood")*(B1:B6="groot")*C1:C6 ) geeft de som van de items in C1:C6 waarvan de items in kolom A zijn "rood" EN waarvan de items in kolom B zijn "groot". A1:A6 en B1:B6 maken elk een matrix van 6 elementen met WAAR of ONWAAR - die in het geval van berekeningen zijn: 1 of 0. Dus als A2 "rood" bevat en B2 bevat "groot" dan is het tweede element van de matrix 1 * 1 * C2 = C2. Als A2 in plaats daarvan "blauw" bevat, wordt het tweede element van de matrix 0 * 1 * C2 = 0.
SOM( (A1:A6="rood")+(B1:B6="groot")*C1:C6 ) geeft de som van de items in C1:C6 waarvan de items in kolom A zijn "rood" OF waarvan de items in kolom B "groot" zijn.
SOM(REST(A1:A6="rood")+(B1:B6="groot")*C1:C6 ) geeft ofwel de som van de items in C1:C6 waarvan de items in kolom A zijn "rood" of waarvan de items in kolom B "groot" zijn, maar niet beide (exclusieve OF)
SOM( NIET(A1:A6="rood")+(B1:B6="groot")*C1:C6 ) geeft de som van de items in C1:C6 waarvan de items in kolom A niet "rood" zijn NOCH waarvan de items in kolom B "groot" zijn.
Tellen van items die overeenkomen met meerdere voorwaarden
SOM( (A1:A6="rood")*(B1:B6="groot") ) geeft het aantal rijen terug waarvan de items in kolom A zijn "rood" EN waarvan de items in kolom B "groot" zijn.
Maximum in een bepaalde maand
MAX(ALS(MAAND(B1:B9)=5; C1:C9; 0)) geeft de maximale waarde terug in C1:C9 waarvan de overeenkomende datum in B1:B9 in Mei is (maand 5). De functie MIN() zou de minimale waarde van die maand teruggeven.
Gemiddelde van items die aan een voorwaarde voldoen
GEMIDDELDE(ALS(A1:A9="rood"; B1:B9; "")) geeft het gemiddelde terug van de items B1:B9 waarvan de items in kolom A “rood” zijn. De functie GEMIDDELDE negeert alle blanco items.
De functie MEDIAAN kan op dezelfde wijze worden gebruikt.
Dynamisch sorteren van een kolom
=GROOTSTE(B3:B9;RIJ(B3:B9)+1-RIJ(B3)) ingevoerd in cel C3 geeft een matrix terug in C3:C9 waarbij B3:B9 in aflopende volgorde staat. +1-RIJ(3) is een constante - u zou in plaats daarvan kunnen schrijven =GROOTSTE(B3:B9;RIJ(B3:B9)-2).
=KLEINSTE(B3:B9;RIJ(B3:B9)-2) geeft B3:B9 terug in oplopende volgorde.
Fouten negeren met SOM
SOM( ALS(ISFOUT(A1:A9); 0; A1:A9) ). Normaal gesproken zal SOM een gevonden fout vermelden.
Gemiddelde, blanco items negeren
GEMIDDELDE(ALS(B1:B9<>0; B1:B9; ""))
Een cel testen op een verzameling waarden
OF(B2={2; 5; 6}) als een matrix-expressie, of OF(B2=2; B2=5; B2=6) als een ‘normale’ formule.
Som van de 4 kleinste getallen
SOM(KLEINSTE(B3:B9; {1;2;3;4})) of SOM(KLEINSTE(B3:B9;RIJ(A1:A4))). RIJ(A1:A4) produceert {1;2;3;4}.
Laatste gebruikte cel in een kolom
MAX(RIJ(B1:B9)*(B1:B9<>"")) geeft het rijnummer terug van de laatste gebruikte cel.
Problemen
- "Matrices als regel" werken in OOo2.3, maar falen als er spaties zijn of negatieve getallen. Dit is opgelost voor OOo2.4, hoewel spaties worden verwijderd in plaats van genegeerd (Issue 82644 ).
- Het zal mogelijk zijn om matrices van verschillende afmetingen op te nemen in een formule, omdat er een gedefinieerd berekeningsproces bestaat in de aanstaande internationale standaard ODFF. Calc zou daar in OOo3.0 aan moeten voldoen (Issue 46681 ).
- Sommige functies kunnen nog niet worden gebruikt in matrixformules: AANTAL.ALS, SOM.ALS (Issue 65866 ); VERGELIJKEN (Issue 8947 ); ISLOGISCH (Issue 87219 ).
- VERSCHUIVING gedraagt zich beperkter binnen een matrixformule.
- Gedefinieerde namen via Invoegen → Namen → Definiëren kunnen worden gebruikt binnen een matrixformule, maar labels (ofwel via Invoegen → Namen → Labels of automatisch herkend boven een kolom) zouden niet moeten worden gebruikt (Issue 87268 ).
- In Excel kunnen niet alle functies worden gebruikt in matrixformules. TEKST.SAMENVOEGEN werkt bijvoorbeeld in Calc wel maar niet in Excel. Wees u bewust van de beperkingen van Excel als u van plan bent om een werkblad van Calc te gebruiken in Excel.
- Functies die snel wijzigen, zoals ASELECT, ASELECTTUSSEN, NU zouden niet opnieuw berekend kunnen worden in matrixformules; bijvoorbeeld in {=A1:A3+ASELECT()} wordt slechts één willekeurig getal gegenereerd (Issue 67135 ).
- Matrixformules kunnen de snelheid van uw computer vertragen als u grote matrices hebt.