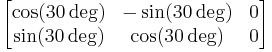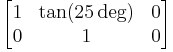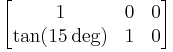Difference between revisions of "User:Regina/MYDrafts4"
((checkpoint save)) |
|||
| Line 2: | Line 2: | ||
== Coordinate System == | == Coordinate System == | ||
| − | There are two common ways to orientate a Cartesian coordinate system | + | There are two common ways to orientate a Cartesian coordinate system. |
{| class="wikitable" | {| class="wikitable" | ||
| Line 44: | Line 44: | ||
Suggestion: | Suggestion: | ||
| − | Example: The value <tt>rotate(30)</tt> corresponds to the transformation matrix <math>\begin{bmatrix}\cos ( | + | Example: The value <tt>rotate(30)</tt> corresponds to the transformation matrix <math>\begin{bmatrix}\cos (30 \deg)& - \sin (30 \deg)&0\\\sin (30 \deg)&\cos (30 \deg)&0 \end{bmatrix}</math> |
[[File:Rotation30deg.png|250px|thumb|left|result of value <tt>rotate(30)</tt>]] | [[File:Rotation30deg.png|250px|thumb|left|result of value <tt>rotate(30)</tt>]] | ||
| Line 54: | Line 54: | ||
Example: The value <tt>scale(0.2 0.5)</tt> corresponds to the transformation matrix <math>\begin{bmatrix}0.2& 0&0\\0&0.5&0 \end{bmatrix}</math> | Example: The value <tt>scale(0.2 0.5)</tt> corresponds to the transformation matrix <math>\begin{bmatrix}0.2& 0&0\\0&0.5&0 \end{bmatrix}</math> | ||
| − | [[File:ScaleX0komma2Y0komma5.png|350px|thumb|left|result of <tt>scale(0.2 0.5)</tt>. Notice that the | + | [[File:ScaleX0komma2Y0komma5.png|350px|thumb|left|result of <tt>scale(0.2 0.5)</tt>. Notice that visually the distances to the axes are scaled too.]] |
|- | |- | ||
| <tt>skewX(skew-angle)</tt>, specifies a skew transformation by <tt>rotate-angle</tt> degrees along the x-axis. | | <tt>skewX(skew-angle)</tt>, specifies a skew transformation by <tt>rotate-angle</tt> degrees along the x-axis. | ||
| Line 63: | Line 63: | ||
Suggestion: | Suggestion: | ||
| − | Example: The value <tt>skewX(25)</tt> corresponds to the transformation matrix <math>\begin{bmatrix}1& \tan ( | + | Example: The value <tt>skewX(25)</tt> corresponds to the transformation matrix <math>\begin{bmatrix}1& \tan (25 \deg)&0\\0&1&0 \end{bmatrix}</math> |
[[File:SkewX25deg.png|250px|thumb|left|A rectangle transformed with <tt>skewX(25)</tt>. This transformation is also known as "shear mapping".]] | [[File:SkewX25deg.png|250px|thumb|left|A rectangle transformed with <tt>skewX(25)</tt>. This transformation is also known as "shear mapping".]] | ||
|- | |- | ||
| <tt>skewY(skew-angle)</tt>, specifies a skew transformation by <tt>rotate-angle</tt> degrees along the y-axis. | | <tt>skewY(skew-angle)</tt>, specifies a skew transformation by <tt>rotate-angle</tt> degrees along the y-axis. | ||
| − | | Same as skewX | + | | Same as skewX, typo "rotate-angle" and unclear angle. |
Suggestion: | Suggestion: | ||
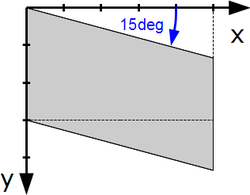
| − | Example: The value <tt>skewY(15)</tt> corresponds to the transformation matrix <math>\begin{bmatrix}1& | + | Example: The value <tt>skewY(15)</tt> corresponds to the transformation matrix <math>\begin{bmatrix}1&0&0\\ \tan(15 \deg)&1&0 \end{bmatrix}</math> |
| − | + | [[File:SkewY15deg.png|250px|thumb|left|A rectangle transformed with <tt>skewY(15)</tt>]] | |
|} | |} | ||
Revision as of 13:04, 9 August 2012
Problems With Angle Definitions in ODF1.2
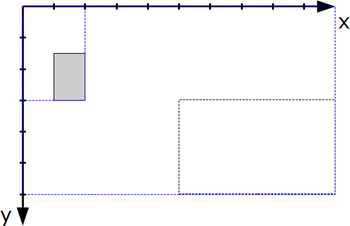
Coordinate System
There are two common ways to orientate a Cartesian coordinate system.
Only when the orientation is determined, terms like "clockwise" are unambigious. Such orientation rule is missing in ODF 1.2.
Suggestion:
If a rule refers to a two-dimensional coordinate system, a Cartesian coordinate system in screen orientation (see figure ##) is used. The directions "clockwise", "counter clockwise", and the edge descriptions "left", "top", "right" and "button" are accordingly defined as shown in figures [##] to [##].
Angles in Attribute draw:transform
These suggestions are all about section 19.228. (Because of the Wiki markup I skipped the characters < and >).
I suggest to give for each single transformation value an example with reference to the corresponding transformation matrix and illustrate that example .
| Original | Problems and Suggestions |
|---|---|
| The whole original text is very near to SVG section 7, but a reference is missing. | |
| matrix(a b c d e f), specifies a transformation in the form of a transformation matrix of six values. "The values describe... | Typo: The quotation mark before 'The values' has to be removed. |
| rotate(rotate-angle), specifies a rotation by rotate-angle degrees about the origin of the shapes coordinate system. | The orientation of the rotation is missing. I suggest not to use "clockwise" but to define it by an equivalent matrix.
Suggestion: Example: The value rotate(30) corresponds to the transformation matrix |
| scale( sx [ sy ]), specifies a scale operation by sx and sy. | It is not clear, that not only the object is scaled.
Suggestion: Example: The value scale(0.2 0.5) corresponds to the transformation matrix |
| skewX(skew-angle), specifies a skew transformation by rotate-angle degrees along the x-axis. | Typo: "rotate-angle" should be "skew-angle".
Here is neither clear between which rays the angle is measured, nor what direction is used. Suggestion: Example: The value skewX(25) corresponds to the transformation matrix |
| skewY(skew-angle), specifies a skew transformation by rotate-angle degrees along the y-axis. | Same as skewX, typo "rotate-angle" and unclear angle.
Suggestion: Example: The value skewY(15) corresponds to the transformation matrix |