Documentation/OOoAuthors User Manual/Writer Guide/Math Objects

Статья в работе (ЧЕРНОВИК), и находится в процессе написания.

This page was created by converting ODT to Mediawiki using Writer2MediaWiki. The page needs cleaning up, and figures added.

This is Chapter 16 of the OpenOffice.org 2.x Writer Guide (Third edition), produced by the OOoAuthors group. A PDF of this chapter is available from the OOoAuthors Guides page at OpenOffice.org.

<< User Manuals page
<< Writer Guide Table of Contents
<< Chapter 15 Using Forms in Writer   |    Appendix A Keyboard Shortcuts >>

Introduction

OpenOffice.org (OOo) has a component for mathematical equations. It is most commonly used as an equation editor for text documents, but it can also be used with other types of documents or stand-alone. When used inside Writer, the equation is treated as an object inside the text document.

The equation editor is for writing equations in symbolic form (as in equation 1). If you want to evaluate a numeric value, see the Calc Guide.

${\frac {df(x)}{dx}}=\ln(x)+\tan ^{-1}(x^{2})$ (1)

Getting started

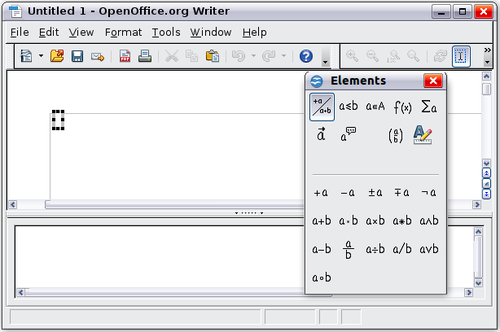
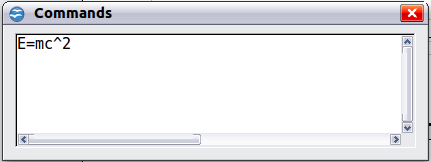
To insert an equation, go to Insert > Object > Formula.

The equation editor opens at the bottom of the screen, and the floating Elements window (called “Selection” before Math 3.2 and “Formula Elements” in Math 3.2) may appear. You will also see a small box (with a gray border) in your document, where the formula will be displayed.

Equation Editor, Elements window, and location of resulting equation.

The equation editor uses a markup language to represent formulas. For example, %beta creates the Greek character beta (β). This markup is designed to read similar to English whenever possible. For example, a over b produces a fraction: ${\frac {a}{b}}$

To insert a numbered formula in Writer, type fn then press the  F3  key.

Additional References

For very basic step-by-step instructions and tutorials for specific tasks, see http://plan-b-for-openoffice.org/math/index

The equation editor uses a markup language to represent formulas. For example, %beta creates the Greek character beta ($\beta$). This markup is designed to read similar to English whenever possible. For example, a over b produces a fraction: $a \over b$.

You can enter a formula in three ways:

• Select a symbol from the Elements window.
• Right-click on the equation editor and select the symbol from the context menu.
• Type markup in the equation editor.

The context menu and the Elements window insert the markup corresponding to a symbol. Incidentally, this provides a convenient way to learn the OOoMath markup.

Click on the document body to exit the formula editor. Double-click on a formula to enter the formula editor again.

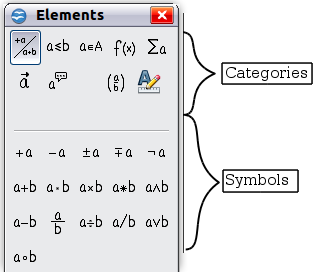
The Elements window

The simplest method for entering a formula is the Elements window, shown below.

Symbols are divided into categories.

The Elements window is divided into two main portions.

• The top shows the symbol categories. Click on these to change the list of symbols.
• The bottom shows the symbols available in the current category.

You can hide (or unhide) the Elements window with View > Elements.

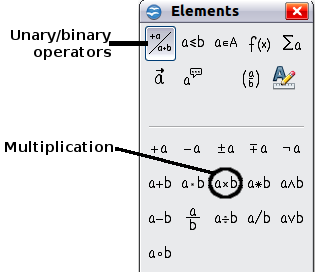
Example 1: 5 × 4

For this example we will enter a simple formula: 5 × 4

On the Elements window:

1. Select the top-left button of the categories (top) section.
2. Click on the multiplication symbol.

Unary/binary operators.

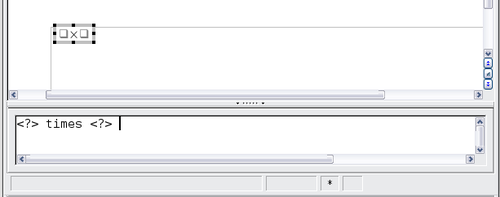
When you select the multiplication symbol on the Elements window, two things happen:

• The equation editor shows the markup: <?> times <?>
• The body of the document shows a gray box with the figure: $\Box \times \Box$

The multiplication symbol.

The <?> symbols are placeholders that you can replace by other text. The equation will update automatically, and the result should resemble the figure below.

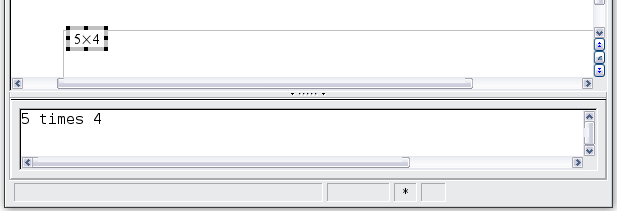
Result of entering "5" and "4" next to the "times" operator.

To keep the equation from updating automatically, select View > AutoUpdate display. To update a formula manually, press F9 or select View > Update.

Right-click menu

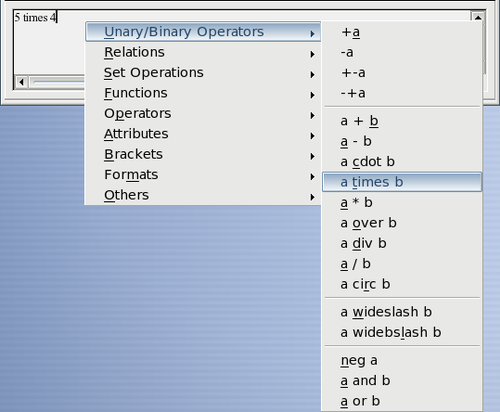
Another way to access mathematical symbols is to right-click on the equation editor. This produces a menu as shown in the figure below.

Right-click menu.

The entries in this menu correspond exactly to those in the Elements window.

Markup

You can type the markup directly in the equation editor. For example, you can type “5 times 4" to obtain $5\times 4$. If you know the markup, this can be the fastest way to enter a formula.

The formula markup resembles the way the formula reads in English.

Below is a short list of common equations and their corresponding markup.

Display	Command	Display	Command
a=b	a = b	√a	sqrt {a}
a2	a^2	an	a_n
∫ f(x)dx	int f(x) dx	∑ an	sum a_n
a≤b	a <= b	∞	infinity
a×b	a times b	x·y	x cdot y

Greek characters

Greek characters (α, β, γ, θ, etc.) are common in mathematical formulas. These characters are not available in the Elements window or the right-click menu. Fortunately, the markup for Greek characters is simple: Type a % sign followed the name of the character, in English.

• To type a lowercase character, write the name of the character in lowercase.
• To type an uppercase character, write the name of the character in uppercase.

See the table below for some examples.

Lowercase	Uppercase
%alpha α	%ALPHA Α
%beta β	%BETA Β
%gamma γ	%GAMMA Γ
%psi ψ	%PSI Ψ
%phi φ	%PHI Φ
%theta θ	%THETA Θ

A complete table of Greek characters is included at the end of the Reference section.

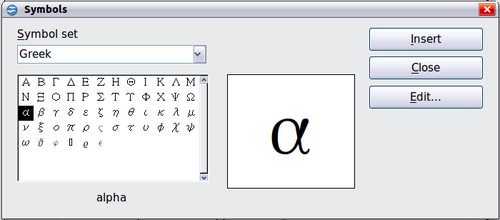
Another way to enter Greek characters is by using the catalog window. Go to Tools > Catalog. The catalog window is shown below. Under “Symbol Set" select “Greek" and double-click on a Greek letter from the list. The markup name of the character is shown below the list window.

Catalog, used for entering Greek characters and some special symbols.

Example 2: π $\simeq \!$ 3.14159

For this example we will suppose that:

• We want to enter the above formula (the value of pi rounded to 5 decimal places).
• We know the name of the Greek character ("pi").
• But we do not know the markup associated with the $\simeq \!$ symbol.

Step 1: Type % followed by the text pi. This displays the Greek character π.

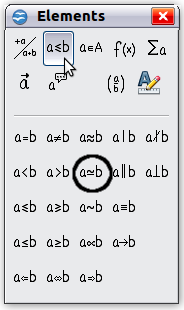
Step 2: Open the Elements window (View > Elements).

Step 3: The $\simeq \!$ symbol is a relation, so we click on the relations button . If you hover the mouse over this button you see the tooltip "Relations".

Tooltip indicates the "Relations" button.

After selecting "Relations".

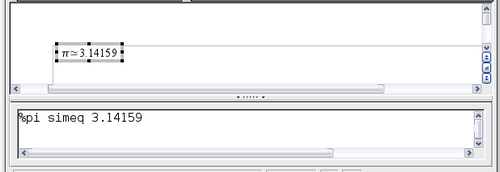
Step 4: Click on the $a\simeq b$ symbol. The equation editor now shows the markup %pi<?> simeq <?>.

Step 5: Delete the <?> text and add 3.14159 at the end of the equation. Hence we end up with the markup %pi simeq 3.14159. The result is shown below.

Final result.

Formula editor as a floating window

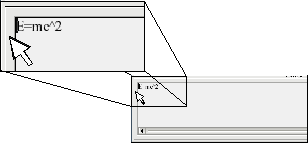
As seen in Figure 1, the formula editor can cover a large part of the Writer window. To turn the formula editor into a floating window, do this:

1. Hover the mouse over the editor frame, as shown below.
2. Hold down the Control key and double-click.

Hold down the Control key and double-click on the border of the math editor to turn it into a floating window.

The figure below shows the result. You can make the floating window back into an embedded frame, using the same steps. Hold down the Control key and double-click the window frame.

Equation editor as a floating window.

How can I make a formula bigger?

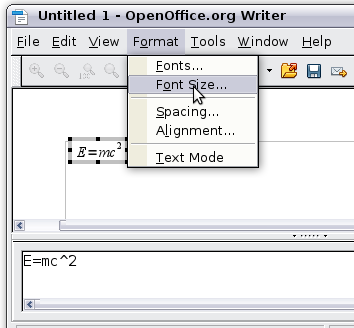
This is one of the most common questions people ask about OOoMath. The answer is simple, but not intuitive:

1. Start the formula editor and go to Format > Font size.

Changing font size for a formula.
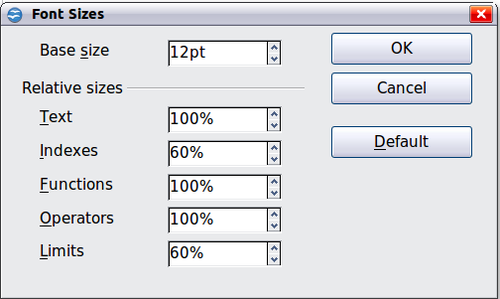
2. Select a larger font size under “Base Size" (top-most entry), as shown below.

Edit Base Size

Edit "Base size" (top) to make a formula bigger.

The result of this change is illustrated below.

Result of changing the base font size.

The most difficult part of using OOo Math comes when writing complicated formulas. This section provides some advice.

Brackets are your friends

OOo Math knows nothing about order of operation. You must use brackets to state the order of operations explicitly. Consider the following example:

Markup	Result
2 over x + 1	${2 \over x}+1$
2 over {x + 1}	$2 \over {x+1}$

Equations over more than one line

Suppose you want to type an equation covering more than one line. For example:

$x=3\,\!$

$y=1\,\!$

Your first reaction would be to simply press the Enter key. However, if you press the Enter key, though the markup goes to a new line, the resulting equation does not. You must type the newline command explicitly. This is illustrated in the table below.

Markup	Result
x = 3 y = 1	$x=3\ y=1$
x = 3 newline y = 1	$x=3\,\!$ $y=1\,\!$

---

See Also

• How do I Align my Equations at the Equality Sign?

How do I add limits to my sum/integral?

The “sum" and “int" commands can (optionally) take in the parameters “from" and “to". These are used for lower and upper limits respectively. These parameters can be used singly or together. Limits for integrals are usually treated as subscripts and superscripts.

Markup	Result
sum from k = 1 to n a_k	$\sum _{k=1}^{n}a_{k}$
int from 0 to x f(t) dt or int_0^x f(t) dt	$\int \limits _{0}^{x}f(t)dt$ or $\int _{0}^{x}f(t)dt$
int from Re f	$\int \limits _{\Re }f$
sum to infinity 2^{-n}	$\sum _{}^{\infty }2^{-n}$

For more details on integrals and sums, see the Math commands reference.

Brackets with matrices look ugly!

For background, we start with an overview of the matrix command:

Markup	Result
matrix { a # b ## c # d }	${\begin{smallmatrix}a&b\\c&d\end{smallmatrix}}$

Rows are separated by two #'s and entries within each row are separated by one #.

The first problem people have with matrices is that brackets do not “scale" with the matrix:

Markup	Result
( matrix { a # b ## c # d } )	(${\begin{smallmatrix}a&b\\c&d\end{smallmatrix}}$)

OOoMath provides “scalable" brackets. That is, the brackets grow in size to match the size of their contents. Use the commands left( and right) to make scalable brackets.

Markup	Result
left( matrix { a # b ## c # d } right)	$\left({\begin{smallmatrix}a&b\\c&d\end{smallmatrix}}\right)$

Use left[ and right] to obtain square brackets.

How do I make a derivative?

Making derivatives essentially comes down to one trick: Tell OOo it's a fraction.

In other words, you have to use the over command. Combine this with either the letter “d" (for a total derivative) or the partial command (for a partial derivative) to achieve the effect of a derivative.

Markup	Result
{df} over {dx}	${\frac {df}{dx}}$
{partial f} over {partial y}	${\frac {\partial f}{\partial y}}$
{partial^2 f} over {partial t^2}	${\frac {\partial ^{2}f}{\partial t^{2}}}$

Notice that we have to use braces (squiggly brackets) to make the derivative.

Numbering equations

Equation numbering is one of OOoMath's best hidden features. The steps are simple, but obscure:

1. Start a new line.
2. Type “fn" and then press F3.

The “fn" is replaced by a numbered formula:

$E=mc^{2}$ (2)

Now you can double-click on the formula to edit it. For example, here is the Riemann Zeta function:

$\zeta (z)=\sum _{n=1}^{\infty }{\frac {1}{n^{z}}}$ (3)

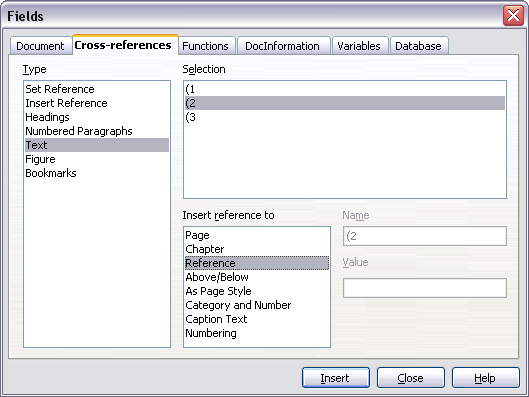
You can reference an equation (“as shown in Equation (2)") with these steps:

1. Insert > Cross-reference..
2. Click on the References tab (Figure 15).
3. Under Type, select Text.
4. Under Selection, pick the equation number.
5. Under Format, choose Reference.
6. Click Insert.

Done! If you later add more equations to the paper before the referenced equation, all the equations will automatically renumber and the cross-references will update.

To insert the equation number without parenthesis around it, choose Numbering under Format instead of Reference.

Math commands - Reference

Unary / binary operators

Operation	Command	Display
+sign	+1	+1
-sign	-1	−1
+/- sign	+-1	±1
-/+ sign	-+1
Boolean not	neg a	¬a
Addition +	a + b	a+b
Multiplication dot	a cdot b	a·b
Multiplication (X)	a times b	a×b
Multiplication (*)	a * b
Boolean and	a and b	a∧b
Subtraction (-)	a - b	a−b
Division (fraction)	a over b
Division (operand)	a div b	a÷b
Division (slash)	a / b	a/b
Boolean or	a or b	a∨b
Concatenate	a circ b

Relational operators

Operation	Command	Display
Is equal	a = b	a=b
Is not equal	a <> b	a≠b
Approximately	a approx 2	a≈b
Divides	a divides b
Does not divide	a ndivides b
Less than	a < 2	a<b
Greater than	a > 2	a>b
Similar to or equal	a simeq b
Parallel	a parallel b
Orthogonal to	a ortho b
Less than or equal to	a leslant b
Greater than or equal to	a geslant b
Similar to	a sim b
Congruent	a equiv b	a≡b
Less than or equal to	a <= b	a≤b
Greater than or equal to	a >= b	a≥b
Proportional	a prop b
Toward	a toward b	a→b
Arrow left	a dlarrow b	a⇐b
Double arrow left and right	a dlrarrow b	a⇔b
Arrow right	a drarrow b	a⇒b

Set operations

Operation	Command	Display
Is in	a in B	a∈B
Is not in	a notin B	a∉B
Owns	A owns b
Empty set	emptyset
Intersection	A intersection B	A∩B
Union	A union B	A∪B
Difference	A setminus B
Quotient	A slash B
Aleph	aleph	ℵ
Subset	A subset B	A⊂B
Subset or equal to	A subseteq B	A⊆B
Superset	A supset B	A⊃B
Superset or equal to	A supseteq B	A⊇B
Not subset	A nsubset B	A⊂ / B
Not subset or equal	A nsubseteq B	A⊆ / B
Not superset	A nsupset B	A⊃ / B
Not superset or equal	A nsupseteq B	A⊇ / B
Set of natural numbers	setN
Set of integers	setZ
Set of rational numbers	setQ
Set of real numbers	setR
Set of complex numbers	setC

Functions

	Operation	Command	Display
	Exponential	func e^{a}	inline:Object114.png
	Natural logarithm	ln(a)	inline:Object115.png
	Exponential function	exp(a)	inline:Object116.png
	Logarithm	log(a)	inline:Object117.png
	Power	a^{b}	inline:Object118.png
	Sine	sin(a)	inline:Object119.png
	Cosine	cos(a)	inline:Object120.png
	Tangent	tan(a)	inline:Object121.png
	Cotangent	cot(a)	inline:Object122.png
	Square root	sqrt{a}	inline:Object123.png
	Arcsine	arcsin(a)	inline:Object124.png
	Arc cosine	arccos(a)	inline:Object125.png
	Arctangent	arctan(a)	inline:Object126.png
	Arc cotangent	arccot(a)	inline:Object127.png
	nth root	nroot{a}{b}	inline:Object128.png
	Hyperbolic sine	sinh(a)	inline:Object129.png
	Hyperbolic cosine	cosh(a)	inline:Object130.png
	Hyperbolic tangent	tanh(a)	inline:Object131.png
	Hyperbolic cotangent	coth(a)	inline:Object132.png
	Absolute value	abs{a}	inline:Object133.png
	Arc hyperbolic sine	arsinh(a)	inline:Object134.png
	Arc hyperbolic cosine	arccosh(a)	inline:Object135.png
	Arc hyperbolic tangent	arctanh(a)	inline:Object136.png
	Arc hyperbolic cotangent	arccoth(a)	inline:Object137.png
	Factorial	fact{a}	inline:Object138.png

Operators

All operators can be used with the limit functions (“from" and “to").

	Operation	Command	Display
	Limit	lim{a}	inline:Object139.png
	Sum	sum{a}	inline:Object140.png
	Product	prod{a}	inline:Object141.png
	Coproduct	coprod{a}	inline:Object142.png
	Upper and lower bounds shown with integral	int from {r_0} to {r_t} a	inline:Object143.png
	Integral	int{a}	inline:Object144.png
	Double integral	iint{a}	inline:Object145.png
	Triple integral	iiint{a}	inline:Object146.png
	Lower bound shown with summation symbol	sum from{3}b	inline:Object147.png
	Contour integral	lint a	inline:Object148.png
	Double curved integral	llint a	inline:Object149.png
	Triple curved integral	lllint a	inline:Object150.png
	Upper bound shown with product symbol	prod to{3} r	inline:Object151.png

Attributes

Operation	Command	Display
Acute accent	acute a
Grave accent	grave a
Reverse circumflex	check a
Breve	breve a
Circle	circle a
Vector arrow	vec a
Tilde	tilde a
Circumflex	hat a
Line above	bar a
Dot	dot a
Wide vector arrow	widevec abc
Wide tilde	widetilde abc
Wide circumflex	widehat abc
Double dot	ddot a
Line over	overline abc
Line under	underline abc
Line through	overstrike abc
Triple dot	dddot a
Transparent (useful to get a placeholder of a given size)	phantom a
Bold font	bold a
Italic font (see Note 1)	ital “a"
Resize font	size 16 qv
Following item in sans serif font (see Note 2)	font sans qv
Following item in serif font	font serif qv
Following item in fixed font	font fixed qv
Make color of following text cyan (see Note 3)	color cyan qv
Make color of following text yellow	color yellow qv
Make color of following text white	color white qv
Make color of following text green	color green qv
Make color of following text blue	color blue qv
Make color of following text red	color red qv
Make color green returns to default color black	color green X qv
Brace items to change color of more than one item	color green {X qv}

Note 1: Unquoted text that is not a command is considered to be a variable. Variables are, by default, italicized.

Note 2: There are three custom fonts: sans serif (without kicks), serifs (with kicks), and fixed (non-proportional). To change the actual fonts used for custom fonts and the fonts used for variables (unquoted text), numbers and functions, use Format > Fonts.

Note 3: For all coloring, the color will apply only to the text immediately following the command until the next space is encountered. In order to have the color apply to more characters, place the text you want in color in curly brackets.

Miscellaneous

Operation	Command	Display
Infinity	infinity
Partial	partial
Nabla	nabla
There exists	exists
For all	forall
H bar	hbar
Lambda bar	lambdabar
Real part	re
Imaginary part	im
Weierstrass p	wp
Left arrow	leftarrow
Right arrow	rightarrow
Up arrow	uparrow
Down arrow	downarrow
Dots at bottom	dotslow
Dots at middle	dotsaxis
Dots vertical	dotsvert
Dots diagonal upward	dotsup
Dots diagonal downward	dotsdown

Brackets

Operation	Command	Display
Round Brackets	(a)	(a)
Square Brackets	[b]	[b]
Double Square Brackets	ldbracket c rdbracket
Single line	lline a rline
Double line	ldline a rdline
Braces	lbrace w rbrace	{w}
Angle Brackets	langle d rangle
Operator Brackets	langle a mline b rangle
Group brackets (used for program control)	{a}
Scalable round brackets (add the word "left" before a left bracket and "right" before a right bracket)	left ( stack{a # b # z} right )
Square brackets scalable (as above)	left [ stack{ x # y} right ]
Double square brackets scalable	left ldbracket c right rdbracket
Line scalable	left lline a right rline
Double line scalable	left ldline d right rdline
Brace scalable	left lbrace e right rbrace
Angle bracket scalable	left langle f right rangle
Operator brackets scalable	left langle g mline h right rangle
Over brace scalable	{The brace is above} overbrace a
Under brace scalable	{the brace is below}underbrace {f}

Formats

Operation	Command	Display
Left superscript	a lsup{b}
Center superscript	a csup{b}
Right superscript	a^{b}
Left subscript	a lsub{b}
Center subscript	a csub{b}
Right subscript	a_{b}
Align character to left (text is aligned center by default)	stack { Hello world # alignl (a) }
Align character to center	stack{Hello world # alignc(a)}
Align character to right	stack { Hello world # alignr(a)}
Vertical stack of 2	binom{a}{b}
Vertical stack, more than 2	stack{a # b # z}
Matrix stack	matrix{a # b ## c # d}
Common mathematical arrangement	matrix{a # "="b ## {} # "="c}
New line	asldkfjo newline sadkfj
Small gap (grave)	stuff `stuff
Large gap (tilde)	stuff~stuff

Characters – Greek

	%ALPHA	inline:Object68.png	%BETA	inline:Object214.png	%CHI	inline:Object215.png	%DELTA	inline:Object216.png	%EPSILON	inline:Object230.png
	%ETA	inline:Object231.png	%GAMMA	inline:Object232.png	%IOTA	inline:Object233.png	%KAPPA	inline:Object234.png	%LAMBDA	inline:Object235.png
	%MU	inline:Object236.png	%NU	inline:Object237.png	%OMEGA	inline:Object238.png	%OMICRON	inline:Object239.png	%PHI	inline:Object240.png
	%PI	inline:Object241.png	%PSI	inline:Object242.png	%RHO	inline:Object243.png	%SIGMA	inline:Object244.png	%THETA	inline:Object245.png
	%UPSILON	inline:Object246.png	%XI	inline:Object247.png	%ZETA	inline:Object248.png
	%alpha	inline:Object249.png	%beta	inline:Object250.png	%chi	inline:Object251.png	%delta	inline:Object252.png	%epsilon	inline:Object253.png
	%eta	inline:Object254.png	%gamma	inline:Object255.png	%iota	inline:Object256.png	%kappa	inline:Object257.png	%lambda	inline:Object258.png
	%mu	inline:Object259.png	%nu	inline:Object260.png	%omega	inline:Object261.png	%omicron	inline:Object262.png	%phi	inline:Object263.png
	%pi	inline:Object276.png	%rho	inline:Object284.png	%sigma	inline:Object285.png	%tau	inline:Object286.png	%theta	inline:Object287.png
	%upsilon	inline:Object288.png	%varepsilon	inline:Object289.png	%varphi	inline:Object290.png	%varpi	inline:Object291.png	%varrho	inline:Object299.png
	%varsigma	inline:Object300.png	%vartheta	inline:Object301.png	%xi	inline:Object302.png	%zeta	inline:Object303.png

Characters – Special

	%and inline:Object344.png	%angle inline:Object272.png	%element inline:Object273.png	%identical inline:Object274.png
	%infinite inline:Object275.png	%noelement inline:Object345.png	%notequal inline:Object346.png	%or inline:Object347.png
	%perthousand inline:Object348.png	%strictlygreaterthan inline:Object349.png	%strictlylessthan inline:Object350.png	%tendto inline:Object351.png